Exemple de sujet
1 boite de petits pics en bois, de la patafix, 1 globe, 1 lampe, Fichier pdf : Document : La Terre est ronde ! Ératosthène et la mesure du rayon terrestre
Complément : Passage du livre de Cléomède De motu circulari corporum coelestium écrit au 1° siècle ap JC.
Et la méthode de Posidonios à propos de la grandeur de la terre est de cette sorte, mais celle d'Eratosthène est dépendante d'une méthode géométrique et semble avoir quelque chose de moins claire. Il rendrait clair ce qu'il a dit si nous les présupposons au préalable. Qu'il soit admis pour nous, premièrement que Syène et Alexandrie sont établies sous le méridien, deuxièmement que la distance entre les deux cités est de 5000 stades, troisièmement que les rayons envoyés de différents endroits du soleil sur différents endroits de la Terre sont parallèles ; en effet, les géomètres supposent qu'il en est ainsi.
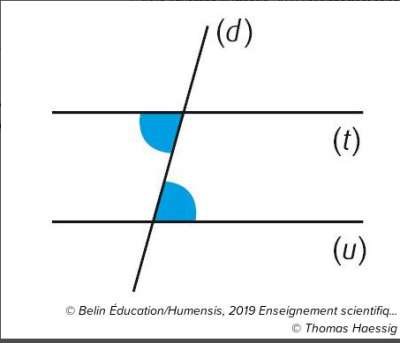
Quatrièmement que ceci soit admis comme démontré auprès des géomètres, que les droites sécantes des parallèles forment des angles alternes égaux, cinquièmement que les arcs de cercle qui reposent sur des angles égaux sont semblables, c'est à dire qu'ils ont la même similitude et le même rapport relativement aux cercles correspondants, ceci étant démontré aussi chez les géomètres. Lorsqu'en effet les arcs de cercle reposent sur des angles égaux, quelque soit l'un (d'entre-eux) s'il est la dixième partie de son propre cercle, tous les autres seront les dixièmes parties de leurs propres cercles. [...]
Et sur cet angle s'appuie l'arc de cercle qui fait le tour de la pointe de l'ombre du gnomon jusqu'à sa base tandis que celui qui est proche du centre de la terre s'appuie l'arc qui va de Syène à Alexandrie. Ces arcs de cercle sont donc semblables l'un à l'autre en s'appuyant sur des côtés égaux. Le rapport qu'a l'arc du cadran avec son propre cercle, l'arc qui va de Syène à Alexandrie a ce rapport aussi. Mais on trouve que l'arc du cadran est la cinquantième partie de son propre cercle. Il faut donc nécessairement que la distance qui va de Syène à Alexandrie soit la cinquantième partie du plus grand cercle de la Terre. Et elle est de 5000 stades. Le cercle dans sa totalité fait donc 250 000 stades. Voilà la méthode d'Eratosthène.
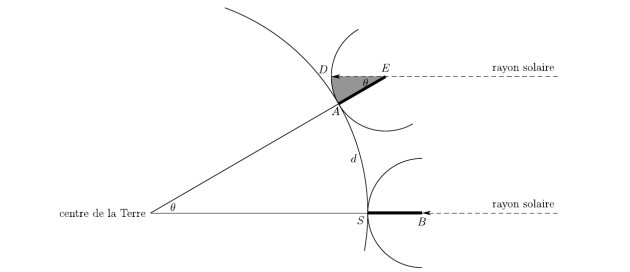
Cléomède poursuit par l’énoncé de quelques faits d’observation : au solstice d’été, sous le tropique du Cancer, les gnomons des cadrans solaires concaves (scaphé) sont nécessairement sans ombre tandis que ceux d’Alexandrie (située au nord de Syène = Assouan) projettent une ombre (figure ci-dessus). Comme les arcs DA et AS sont limités par des angles égaux, ils délimitent une portion de cercle identique (présupposé n°5). La portion d’arc formée par l’ombre du gnomon de la scaphé située à Alexandrie est donc égale à la portion d’arc délimitée par la ligne Syène-Alexandrie. Autrement dit, l’arc qui va de Syène à Alexandrie représente une portion du cercle terrestre identique à celle du cercle de la scaphé délimitée par l’ombre du gnomon d’Alexandrie.
Sur la figure ci-dessous, S localise la ville de Syène et A celle d’Alexandrie, l’arc AD est égal à 1/50e du cercle de centre E et de rayon [EA], les angles θ aux sommets E et O (centre de la Terre) sont égaux, l’arc AS délimite donc également 1/50e du cercle terrestre). Notons que le texte ne mentionne pas le calcul du rayon terrestre qui ne peut en aucun cas, compte-tenu des connaissances de l’époque, précéder celui du périmètre de la Terre.
Attention : Méthode utilisée par les ouvrages du secondaire
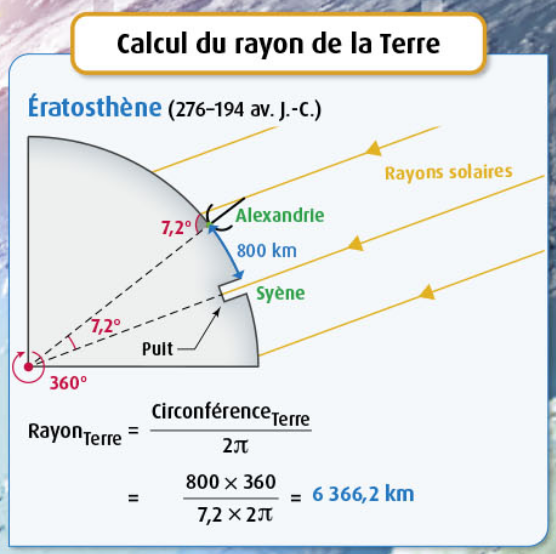
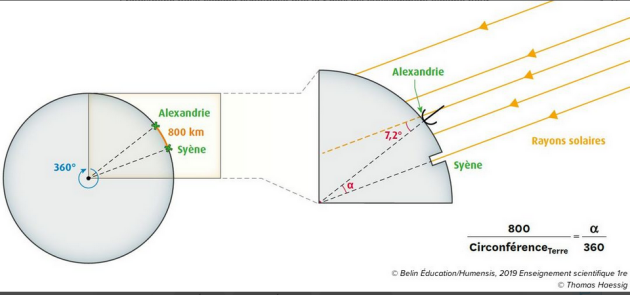
On donne l'angle de 7.2° sans préciser sa méthode d'obtention, on calcule ensuite le rayon de la Terre en utilisant la valeur de l'angle entre les rayons du soleil et le bâton pour retrouver ce qui avait réellement été observé (1/50e de cercle = 360/7.2). Les éléments de géométrie utilisés n'étaient pas connus à l'époque d'Erastothène. Il y a ici une transposition didactique. En effet les élèves pourront retrouver l'angle en mesurant l'ombre et la hauteur du bâton du gnomon et trouveront que tan alpha = lg ombre/lg bâton
Remarque : historiquement on ne sait pas comment la distance entre Sienne et Alexandrie a été estimée.